In general, if the random variable K follows the binomial distribution with parameters n and p, we write K ~ B(n, p). The probability of getting exactly k successes in n trials is given by the probability mass function:

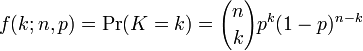
f(k;n,p) = \Pr(K = k) = {n\choose k}p^k(1-p)^{n-k}

for k = 0, 1, 2, ..., n, where

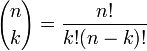
{n\choose k}=\frac{n!}{k!(n-k)!}

 

The cumulative distribution function can be expressed as:

 

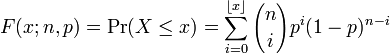
F(x;n,p) = \Pr(X \le x) = \sum_{i=0}^{\lfloor x \rfloor} {n\choose i}p^i(1-p)^{n-i}

 

Where is the "floor" under x, i.e. the greatest integer less than or equal to x.

 

Now, in this problem we have the following values.

 

P(X<=2), n=6, p=0.4

 

If we plug these into the cumulative distribution function we get the following result:

 

(1)(.4)0(0.6)6  + (6!/1!5!)(0.4)1(0.6)5   +  (6!/2!4!)(0.4)2(0.6)4

 

(1)(1)(0.046656)  +  (6)(.4)(0.07776)  +  ((6)(5)/(2))(0.16)( 0.1296)

 

0.544