Calculus Study Material
Home | About Us | estore | FAQ'S | Contact Us | Student Login
Online Tutors Homework Help Pricing Free Video Library Blog
Calculus Study Material

Calculus Video Tutorials, Online Lessons, Ebooks

Video Tutorials under Calculus

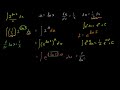  • (2^ln x)/x Antiderivative Example Video Tutorial
    (2^ln x)/x Antiderivative Example
  • Another u-Subsitution Example Video Tutorial
    Another u-Subsitution Example
  • AP Calculus BC Exams: 2008 1 A Video Tutorial
    AP Calculus BC Exams: 2008 1 A
  • AP Calculus BC Exams: 2008 1 B Video Tutorial
    AP Calculus BC Exams: 2008 1 B
  • AP Calculus BC Exams: 2008 1 C Video Tutorial
    AP Calculus BC Exams: 2008 1 C
  • AP Calculus BC Exams: 2008 1 D Video Tutorial
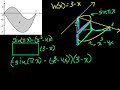    AP Calculus BC Exams: 2008 1 D
  • Calculus BC 2008 2 A Video Tutorial
    Calculus BC 2008 2 A
  • Calculus BC 2008 2 B & C Video Tutorial
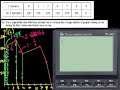    Calculus BC 2008 2 B & C
  • Calculus BC 2008 2 D Video Tutorial
    Calculus BC 2008 2 D
  • Calculus Graphing with Derivatives Example Video Tutorial
    Calculus Graphing with Derivatives Example
  • Calculus: Derivative of x^(x^x) Video Tutorial
    Calculus: Derivative of x^(x^x)
  • Calculus: Derivatives 1 Video Tutorial
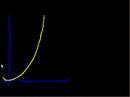    Calculus: Derivatives 1
  • Calculus: Derivatives 2 Video Tutorial
    Calculus: Derivatives 2
  • Calculus: Derivatives 3 Video Tutorial
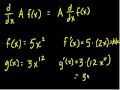    Calculus: Derivatives 3
  • Calculus: Derivatives 4: The Chain Rule Video Tutorial
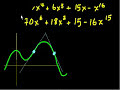    Calculus: Derivatives 4: The Chain Rule
  • Calculus: Derivatives 5 Video Tutorial
    Calculus: Derivatives 5
  • Calculus: Derivatives 6 Video Tutorial
    Calculus: Derivatives 6
  • Calculus: Derivatives 7 Video Tutorial
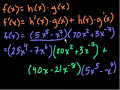    Calculus: Derivatives 7
  • Calculus: Derivatives 8 Video Tutorial
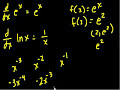    Calculus: Derivatives 8
  • Calculus: Derivatives 9 Video Tutorial
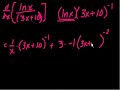    Calculus: Derivatives 9
  • Calculus: Graphing Using Derivatives Video Tutorial
    Calculus: Graphing Using Derivatives
  • Calculus: Maximum and minimum values on an interval Video Tutorial
    Calculus: Maximum and minimum values on an interval
  • Closed Curve Line Integrals of Conservative Vector Fields Video Tutorial
    Closed Curve Line Integrals of Conservative Vector Fields
  • Curl 1 Video Tutorial
    Curl 1
  • Curl 2 Video Tutorial
    Curl 2
  • Curl 3 Video Tutorial
    Curl 3
  • Definite Integral with Substitution Video Tutorial
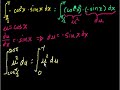    Definite Integral with Substitution
  • Definite Integrals (Area Under a Curve) – Part 3 Video Tutorial
    Definite Integrals (Area Under a Curve) – Part 3
  • Definite Integrals – Part 2 Video Tutorial
    Definite Integrals – Part 2
  • Definite Integrals – Part 4 Video Tutorial
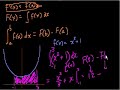    Definite Integrals – Part 4
  • Definite Integrals – Part 5 Video Tutorial
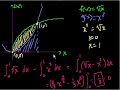    Definite Integrals – Part 5
  • Derivative of a Position Vector Valued Function Video Tutorial
    Derivative of a Position Vector Valued Function
  • Determining a Position Vector-Valued Function for a Parametrization of Two Parameters Video Tutorial
    Determining a Position Vector-Valued Function for a Parametrization of Two Parameters
  • Differential of a vector valued function Video Tutorial
    Differential of a vector valued function
  • Divergence 1 Video Tutorial
    Divergence 1
  • Divergence 2 Video Tutorial
    Divergence 2
  • Divergence 3 Video Tutorial
    Divergence 3
  • Double Integrals 1 Video Tutorial
    Double Integrals 1
  • Double Integrals 2 Video Tutorial
    Double Integrals 2
  • Double Integrals 3 Video Tutorial
    Double Integrals 3
  • Double Integrals 4 Video Tutorial
    Double Integrals 4
  • Double Integrals 5 Video Tutorial
    Double Integrals 5
  • Double Integrals 6 Video Tutorial
    Double Integrals 6
  • Epsilon Delta Limit Definition 1 Video Tutorial
    Epsilon Delta Limit Definition 1
  • Epsilon Delta Limit Definition 2 Video Tutorial
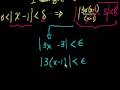    Epsilon Delta Limit Definition 2
  • Equation of a tangent line Video Tutorial
    Equation of a tangent line
  • Example of Calculating a Surface Integral – Part 1 Video Tutorial
    Example of Calculating a Surface Integral – Part 1
  • Example of Calculating a Surface Integral – Part 2 Video Tutorial
    Example of Calculating a Surface Integral – Part 2
  • Example of Calculating a Surface Integral – Part 3 Video Tutorial
    Example of Calculating a Surface Integral – Part 3
  • Example of Closed Line Integral of Conservative Field Video Tutorial
    Example of Closed Line Integral of Conservative Field
  • Exponential Growth Video Tutorial
    Exponential Growth
  • Extreme Derivative Word Problem (Advanced) Video Tutorial
    Extreme Derivative Word Problem (Advanced)
  • Gradient 1 Video Tutorial
    Gradient 1
  • Green’s Theorem Example 1 Video Tutorial
    Green’s Theorem Example 1
  • Green’s Theorem Example 2 Video Tutorial
    Green’s Theorem Example 2
  • Green’s Theorem Proof – Part 1 Video Tutorial
    Green’s Theorem Proof – Part 1
  • Green’s Theorem Proof – Part 2 Video Tutorial
    Green’s Theorem Proof – Part 2
  • Implicit Differentiation – part 2 Video Tutorial
    Implicit Differentiation – part 2
  • Indefinite integrals – part II Video Tutorial
    Indefinite integrals – part II
  • Indefinite Integration – Part III Video Tutorial
    Indefinite Integration – Part III
  • Indefinite Integration – Part IV Video Tutorial
    Indefinite Integration – Part IV
  • Indefinite Integration – Part V Video Tutorial
    Indefinite Integration – Part V
  • Indefinite Integration – Part VI Video Tutorial
    Indefinite Integration – Part VI
  • Indefinite Integration – Part VII Video Tutorial
    Indefinite Integration – Part VII
  • Inflection Points and Concavity Intuition Video Tutorial
    Inflection Points and Concavity Intuition
  • Integrals: Trig Substitution 1 Video Tutorial
    Integrals: Trig Substitution 1
  • Integrals: Trig Substitution 2 Video Tutorial
    Integrals: Trig Substitution 2
  • Integrals: Trig Substitution 3 (Long Problem) Video Tutorial
    Integrals: Trig Substitution 3 (Long Problem)
  • Introduction to Definite Integrals Video Tutorial
    Introduction to Definite Integrals
  • Introduction to Differential Equations Video Tutorial
    Introduction to Differential Equations
  • Introduction to Limits Video Tutorial
    Introduction to Limits
  • Introduction to Parametrizing a Surface with Two Parameters Video Tutorial
    Introduction to Parametrizing a Surface with Two Parameters
  • Introduction to rate-of-change problems Video Tutorial
    Introduction to rate-of-change problems
  • Introduction to the Surface Integral Video Tutorial
    Introduction to the Surface Integral
  • L’Hopital’s Rule – An Introduction Video Tutorial
    L’Hopital’s Rule – An Introduction
  • L’Hopital’s Rule Example 1 Video Tutorial
    L’Hopital’s Rule Example 1
  • L’Hopital’s Rule Example 2 Video Tutorial
    L’Hopital’s Rule Example 2
  • L’Hopital’s Rule Example 3 Video Tutorial
    L’Hopital’s Rule Example 3
  • Ladder rate-of-change problem Video Tutorial
    Ladder rate-of-change problem
  • Limit Examples – Part 1 Video Tutorial
    Limit Examples – Part 1
  • Limit Examples – Part 2 Video Tutorial
    Limit Examples – Part 2
  • Limit Examples – Part 3 Video Tutorial
    Limit Examples – Part 3
  • Limit Examples with Brain Malfunction on First Problem – Part 4 Video Tutorial
    Limit Examples with Brain Malfunction on First Problem – Part 4
  • Line Integral Video Tutorial
    Line Integral
  • Line Integral Example 1 Video Tutorial
    Line Integral Example 1
  • Line Integral Example 2 – Part 1 Video Tutorial
    Line Integral Example 2 – Part 1
  • Line Integral Example 2 – Part 2 Video Tutorial
    Line Integral Example 2 – Part 2
  • Line Integrals & Vector Fields Video Tutorial
    Line Integrals & Vector Fields
  • Maxima Minima Slope Intuition Video Tutorial
    Maxima Minima Slope Intuition
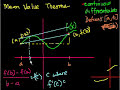  • Mean Value Theorem Video Tutorial
    Mean Value Theorem
  • Monotonicity Theorem Video Tutorial
    Monotonicity Theorem
  • More chain rule and implicit differentiation intuition Video Tutorial
    More chain rule and implicit differentiation intuition
  • More implicit differentiation Video Tutorial
    More implicit differentiation
  • More Limits Video Tutorial
    More Limits
  • Optimization Example 4 Video Tutorial
    Optimization Example 4
  • Optimization with Calculus 1 Video Tutorial
    Optimization with Calculus 1
  • Optimization with Calculus 2 Video Tutorial
    Optimization with Calculus 2
  • Optimization with Calculus 3 Video Tutorial
    Optimization with Calculus 3
  • Parametrization of a Reverse Path Video Tutorial
    Parametrization of a Reverse Path
  • Partial Derivatives Video Tutorial
    Partial Derivatives
  • Partial Derivatives 2 Video Tutorial
    Partial Derivatives 2
  • Partial Derivatives of Vector-Valued Functions Video Tutorial
    Partial Derivatives of Vector-Valued Functions
  • Path Independence for Line Integrals Video Tutorial
    Path Independence for Line Integrals
  • Polynomial Approximation of Functions – Part 1 Video Tutorial
    Polynomial Approximation of Functions – Part 1
  • Polynomial Approximation of Functions – Part 2 Video Tutorial
    Polynomial Approximation of Functions – Part 2
  • Polynomial Approximation of Functions – Part 3 Video Tutorial
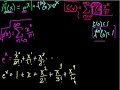    Polynomial Approximation of Functions – Part 3
  • Polynomial Approximation of Functions – Part 4 Video Tutorial
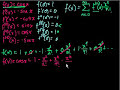    Polynomial Approximation of Functions – Part 4
  • Polynomial Approximation of Functions – Part 5 Video Tutorial
    Polynomial Approximation of Functions – Part 5
  • Polynomial Approximation of Functions – Part 6 Video Tutorial
    Polynomial Approximation of Functions – Part 6
  • Polynomial Approximation of Functions – Part 7 Video Tutorial
    Polynomial Approximation of Functions – Part 7
  • Position Vector Valued Functions Video Tutorial
    Position Vector Valued Functions
  • Proof: d/dx(e^x) = e^x Video Tutorial
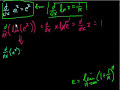    Proof: d/dx(e^x) = e^x
  • Proof: d/dx(ln x) = 1/x Video Tutorial
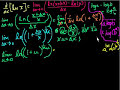    Proof: d/dx(ln x) = 1/x
  • Proof: d/dx(sqrt(x)) Video Tutorial
    Proof: d/dx(sqrt(x))
  • Proof: d/dx(x^n) Video Tutorial
    Proof: d/dx(x^n)
  • Proof: lim (sin x)/x Video Tutorial
    Proof: lim (sin x)/x
  • Proofs of Derivatives of Ln(x) and e^x Video Tutorial
    Proofs of Derivatives of Ln(x) and e^x
  • Rates-of-change – part 2 Video Tutorial
    Rates-of-change – part 2
  • Scalar Field Line Integral Independent of Path Direction Video Tutorial
    Scalar Field Line Integral Independent of Path Direction
  • Second Example of Line Integral of Conservative Vector Field Video Tutorial
    Second Example of Line Integral of Conservative Vector Field
  • Sequences & Series – Part 2 Video Tutorial
    Sequences & Series – Part 2
  • Solid of Revolution – Part 1 Video Tutorial
    Solid of Revolution – Part 1
  • Solid of Revolution – Part 2 Video Tutorial
    Solid of Revolution – Part 2
  • Solid of Revolution – Part 3 Video Tutorial
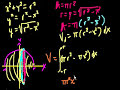    Solid of Revolution – Part 3
  • Solid of Revolution – Part 4 Video Tutorial
    Solid of Revolution – Part 4
  • Solid of Revolution – Part 5 Video Tutorial
    Solid of Revolution – Part 5
  • Solid of Revolution – Part 6 Video Tutorial
    Solid of Revolution – Part 6
  • Solid of Revolution – Part 7 Video Tutorial
    Solid of Revolution – Part 7
  • Solid of Revolution – Part 8 Video Tutorial
    Solid of Revolution – Part 8
  • Squeeze Theorem Video Tutorial
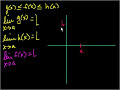    Squeeze Theorem
  • Taylor Polynomials Video Tutorial
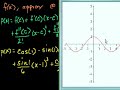    Taylor Polynomials
  • The Indefinite Integral or Anti-derivative Video Tutorial
    The Indefinite Integral or Anti-derivative
  • Trig Implicit Differentiation Example Video Tutorial
    Trig Implicit Differentiation Example
  • Triple Integrals 1 Video Tutorial
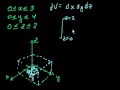    Triple Integrals 1
  • Triple Integrals 2 Video Tutorial
    Triple Integrals 2
  • Triple Integrals 3 Video Tutorial
    Triple Integrals 3
  • Using a Line Integral to find the Work Done by a Vector Field Example Video Tutorial
    Using a Line Integral to find the Work Done by a Vector Field Example
  • Vector Field Line Integrals Dependent on Path Direction Video Tutorial
    Vector Field Line Integrals Dependent on Path Direction
  • Vector Valued Function Derivative Example Video Tutorial
    Vector Valued Function Derivative Example


Register FREE for homework help and online tutoring

First Name
Last Name
Email
Subject/Grade
School
State
Country

  • Search

  • Recently Searched Topics

    • help calculus
    • precalculus help
    • help precalculus
    • homework help calculus
    • free calculus help
    • pre calculus help
    • help with calculus
    • online calculus help
    • math help calculus
    • ap calculus help
    • math calculus help
    • precalculus homework help
    • precalculus help online
    • precalculus graphical numerical algebraic

  • From the Blog

    • How to Use Online Tutoring to Score Better Grades
    • Ways to Get Free Homework Help
    • Schooltrainer.com launches Video Ebooks Library on Facebook
    • How to Prepare for End-Term Exams: 7 Step Strategy
    • One hundred bushels of corn are to be divided among 100 persons. men get 3 bushels each, women 2 and children 1/2. how many men, women and children are present?
Home|About Us|estore|FAQ'S|Contact Us|Student Login